PID Loop (PID) Instruction

Mnemonic (Keyboard Shortcut) = PID

Icon / Button =

Purpose

A Proportional-Integral-Derivative algorithm is a generic Control Loop feedback formula widely used in industrial control systems. A PID algorithm attempts to correct the Error between a measured process variable and a desired setpoint by calculating and then outputting a corrective action that can adjust the process accordingly and rapidly, to keep the Error to a minimum.

What is PID?

Instruction Parameters

Parameter	Parameter Type	Requirements	Description
Enable	Boolean Ladder Rung Input	A Ladder Rung with an Enable contact is required to execute.	Level-driven. When Enable is ON, the instruction will operate every scan. When Enable is OFF, the instruction is not solved and its outputs are not updated.
Manual/Auto	Boolean Ladder Rung Input	Must Have	OFF is Manual Mode. ON is Auto Mode. In Manual Mode, PID calculations are made, but the Process Output is not updated. When the Process is ready to be controlled by the PID instruction, switch to Auto Mode. Initialization Mode settings determine how the loop handles the change-over. Note: It is expected that when the loop is in Manual Mode that an operator or other intelligent source is manually controlling the output by observing the PV and writing data to the output as necessary to keep the process under control.
Configuration Tabs	All the Parameters available to configure a PID Loop are broken down into Configuration Tabs. Each Tab provides Parameters to configure the PID Loop at different levels from a Basic PID Loop to more elaborate PID Loops. The following list shows the available Configuration Tabs and each is described below and linked for quick reference. 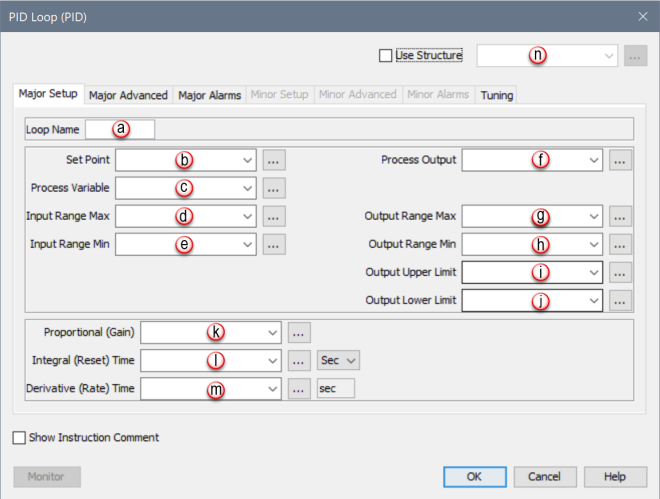Major Setup Tab Major Advanced Tab Major Alarms Tab Minor Tabs are only active when Cascade Mode is selected) Minor Setup Tab Minor Advanced Tab Minor Alarms Tab

Major Setup Tab: Most parameters required to configure a basic PID Loop are located here.

Major Setup Tab Parameters

Parameter	Parameter Type	Requirements	Description
Loop Name	Constant	Must Have	Identifies this PID Loop.
Set Point	Numerical Tag	Must Have	The desired setting for the Process being controlled.
Process Variable	Numerical Tag	Must Have	A Feedback Signal that monitors the current state of the Process.
Input Range Max	Numerical Tag/ Constant	Must Have	The reference point that represents 100% in calculating the scaling factor to apply to the measured Error (SP-PV) before PID calculations. This value will not clamp the inputs. Typical value is the maximum possible input. See Note 1 below.
Input Range Min	Numerical Tag/ Constant	Must Have	The reference point that represents 0% in calculating the scaling factor to apply to the measured Error (SP-PV) before PID calculations. This value will not clamp the inputs. Typical value is the minimum possible input. See Note 1 below.
Process Output	Numerical Tag	Must Have	The result of the Loop Calculation, which drives the Process to the desired Set Point.
Output Range Max	Numerical Tag/ Constant	Must Have if Analog out selected.	The reference point that represents 100% in calculating the scaling factor to apply to the Process Output after PID calculations. This value will not clamp the Process Output. Typical value is the maximum possible Output. See Note 1 and Note 2 below.
Output Range Min	Numerical Tag/ Constant	Must Have if Analog out selected.	The reference point that represents 0% in calculating the scaling factor to apply to the Process Output after PID calculations. This value will not clamp the Process Output. Typical value is the minimum possible Output. See Note 1 below.
Output Upper Limit	Numerical Tag/ Constant	Must Have	Process Output will be clamped to no greater than this value. Typical value is the maximum possibleOutput. See Note 1 below.
Output Lower Limit	Numerical Tag/ Constant	Must Have	Process Output will be clamped to no less than this value. Typical value is the minimum possible Output. See Note 1 below.
Proportional (Gain)	Numerical Tag	Must Have	This value is directly Proportional to the control effect, meaning an increase to the Proportional value (sometimes referred to as Gain) will increase the control output for forward acting Loops and decrease the control output for reverse acting Loops. In the PID Algorithm, the Proportional Gain is multiplied by the Error during each sample and added to the Bias Term. Formula: Pgain * Error (SP-PV) Where: Pgain = Proportional Gain Error = The value difference between Process Variable (PV) and Setpoint (SP). SP = Set Point is the desired Setting for the controlled Process. PV = Process Variable is the Feedback Signal that monitors the current state of the Process. See Note 3 below.
Integral (Reset) Time	Numerical Tag	Must Have	This value is a Time constant that is used to remove Error after the control output has reached a steady state. The Integral Time setting isInverselyProportional to the control effect, meaning as the value increases, the rate at which the Error is removed decreases. In the PID Algorithm, the Integral Term is multiplied by the accumulated Error and added to the control output. Formula: C_{IT } ∑e Where: C_IT = Coefficient of Integral Time ∑e = Summation of Error per sample Note:* To minimize the effect of the Integral Term, give the tag assigned to it a very large initial value. Since the value is Inversely proportional to its effect on the calculation, this will effectively disable it. A zero in the Integral Term gives the maximum possible control effect. Also, See Note 3 below.
Derivative (Rate) Time	Numerical Tag	Optional	In many cases this parameter is not required to achieve stable Loop operation and is highly sensitive to noise in the Error Term. This value is directly Proportional to the control effect, meaning that the higher the Derivative Term setting, the quicker the Error will be removed. In the PID Algorithm, the Derivative Term formula is added to the control output. Formula: C_{DT }e + Initial Output Where: C_DT = Coefficient of Derivative Time e = Current Error - Previous Error See Note 3 below*.

Note 1: This value will be read by the instruction only during an OFF to ON transition of the Enable.

Note 2: To see a change in the Process Output, a value greater than zero must be entered into this parameter.

Note 3: Using a Floating Point tag(s) for the P, I, & D fields allows tighter precision for maximum control.

Major Setup Tab Configuration

When PID Loop Instruction is selected the PID Loop Configuration window shown below opens with the Major Setup Tab opened by default.

Parameter Configuration Table

Instruction

(PID)

Major Setup Tab

Notes

Loop Name

Enter a Name to identify the Loop.

Set Point

Enter a Tag for the Set Point.

Process Variable

Enter a Tag for the Process Variable.

Input Range Max

Enter a Value or Tag for Input Range Max.

Input Range Min

Enter a Value or Tag for Input Range Min.

Process Output

Enter a Tag for the Process Output.

Output Range Max

Enter a Value or Tag for Output Range Max.

Output Range Min

Enter a Value or Tag for Output Range Min.

Output Upper Limit

Enter a Value or Tag for Output Upper Limit.

Output Lower Limit

Enter a Value or Tag for Output Lower Limit.

Proportional (Gain)

Enter a Tag for Proportional Gain.

Integral (Reset)Time

Enter a Tag for Integral Time. Select Seconds or Minutes.

Derivative (Rate) Time

Enter a Tag for Derivative Time.

Use Structure

Select to use a Predefined Structure for this instruction.

Major Advanced Tab Parameters (Common configuration parameters for more Advanced applications)

Parameter	Parameter Type	Requirements	Description
Sample Rate (ms)	Numerical Tag/ Constant	Must Have	Identifies how often the instruction will calculate a new output value. Setting the Sample Rate shorter than the scan time will cause the loop to calculate on every scan. The sample rate must be longer than the rate at which new PV data is available. If it is not, the Integral and Derivative affects could be erratic.
Error Squared	Boolean Tag / Constant	Optional	Setting this bit will Square the Error. This can be useful for many processes by effectively diminishing the control effect on smaller Errors while maintaining the control effect on larger Errors. This can also be useful for reducing the effect of low frequency electrical noise in your process.
Loop Offset (ms)	Numerical Tag/ Constant	Must Have if Auto Mode is not selected	When set to Auto Mode, the CPU attempts to stagger the execution of PID Loops so they will occur on different scans. Loop Offset can be handled manually by assigning different Offset values to multiple PID Loops.
Process Output Percentage	Numerical Tag	Optional	The current Output Percentage on a scale of 0-100%.
Derivative Limit	Numerical Tag/ Constant	Optional	Multiplier that limits the Output adjustment applied by the Derivative term. 1 = 100% of Output scale, or No Limit (default). 0.5 = 50% of Output scale.
Bias Term	Numerical Tag	Optional	The Bias Term is the Current Integral Term + Initial Output. The Bias Term is a value calculated by the instruction, which effectively creates a working region for the Control Output.
Freeze Bias	Radio Button	Optional	Default Setting in ON. Stops the Bias Term calculation when the Output value reaches the upper or lower limit (usually due to a disturbance). This setting prevents reset wind-up which can lead to overshooting the Set Point when a disturbance is removed.
Back Calculation	Radio Button	Optional	If the Output is calculated to be above or below the upper or lower limit, this option will adjust the Bias Term accordingly to make the Output equal to the limit. As soon as the process begins to recover, the loop will go directly into regulation. This anti-windup option is more conservative than Freeze Bias, typically less likely to overshoot but slower to recover from the disturbance.
Base the Derivative on Process Variable	Selectable Checkbox	Optional	When selected, the Derivative is based on changes in the Process Variable. When deselected the Derivative is based on changes in the Error term (SP – PV).
SP Accel Gain	Numerical Tag/ Constant	Optional	A value of 0 disables this function. The process monitors for a change in the set point value. If a set point change is detected, the difference from the new and old set points are multiplied by the SP Accel Gain value and then added to the Bias Term. This action is Edge triggered so it processes only once per change in the set point value.
Error Deadband	Numerical Tag	Optional	When used, the Error Deadband takes a range of Error and substitutes Zero as the value of the Error. Enter the value in Input Units.
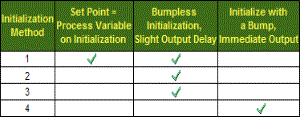
Initialization Mode	Selectable Drop-down List	Check the PV Tracking checkbox or Select one from the list	Determine the state of the Process Variable and Bias Term at startup. SP = PV and Bias = Output. PV tracking check box selected. SP unchanged and Bias = Output SP unchanged and *Bias = (Output – KE) [Default] (where K = The Proportional Term and E = The Error Term) SP unchanged and Bias = Current (initialize with a Bump**)
Process Action	Selectable Drop-down List	Select one from the list	Determines how the Process reacts to the Output. The two choices are: Forward: As the Output increases so will the Process Variable. (i.e., heating loop) Reverse: As the Output increases the Process Variable will decrease. (i.e., cooling loop)
Cascade Mode	Selectable Checkbox	Click on the checkbox to activate Cascade Mode	When selected, Enables the Minor Loop configuration tabs within the PID Loop instruction setup. The first Loop is commonly referred to as the Major Loop or Outer Loop and the Second Loop is commonly referred to as the Minor Loop or Inner Loop. (See Cascade Mode later on in this section).
Enable Control	Boolean Tag	Optional	Level Driven. When this Tag is ON the Output of the Major Loop is redirected as the set point signal of the Minor Loop. When this Tag is OFF, the Minor Loop functions independently and uses the Auto Mode SP Tag as the set point. The ladder Input Manual/Auto must be ON when Enable Control is turned ON. Enable Control will have no effect if Manual/Auto is OFF.

Major Advanced Tab Configuration

When PID Loop Instruction is selected the PID Loop Configuration window opens with the Major Setup Tab opened by default. Click on the Major Advanced Tab to see the Configuration options for Major Advanced shown below.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Major Advanced Tab

Notes

Sample Rate (ms)

Enter a Value or Tag for Sample Rate.

Loop Offset (ms)

Only active if the Auto checkbox is not checked. Enter a Value or Tag for Loop Offset.

Auto

Click checkbox to let the program provide this value Automatically.

Derivative Limit

Enter a Value or Tag for the Derivative Limit.

Bias Term

Enter a Tag for Bias Term.

SP Acceleration Gain

Enter a Value or Tag for SP Acceleration Gain.

Error Deadband

Enter a Value or Tag for Error Deadband.

Process Action

Select a Process Action from the drop-down list. The choices are Forward or Reverse.

Error Squared

Enter a Value (0 or 1) or Tag for Error Squared.

Process Output Percentage

Enter a Tag for Process Output Percentage.

Freeze Bias

Click ON or OFF button to enable or disable this feature.

Back Calculation

Click button to enable this feature.

Base Derivative on Process Variable

Click checkbox to enable this feature.

Initialization Mode: PV Tracking

Click checkbox to select PV tracking method.

Initialization Mode: Unchecked

Select a PV Tracking Mode from the drop-down list.

Cascade Mode

Click checkbox to activate Cascade Mode.

Enable Control

Enter a Value (0 or 1) or Boolean Tag for Enable Control.

Use Structure

Select to use a Predefined Structure for this instruction.

Major Alarms Tab

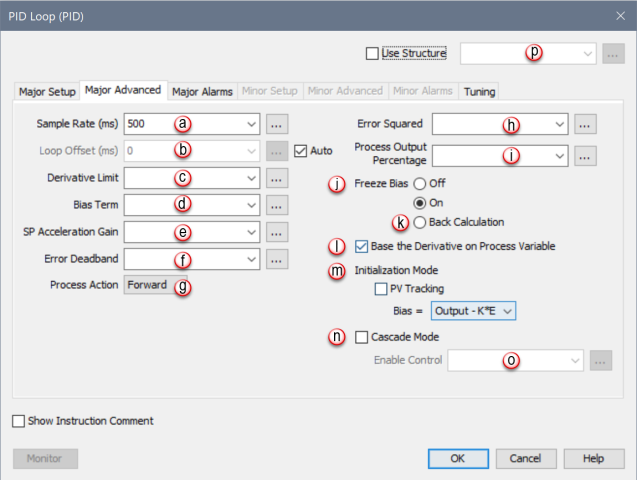
This Tab provides Configuration for Major PID Alarm condition Tags.

Major Alarms Tab Parameters

Parameter	Parameter Type	Requirements	Description
High High Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Greater Than or Equal To this value, the High High Limit Bit will turn ON.
High High Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Greater Than or Equal To the High High Limit parameter setting.
High Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Greater Than or Equal To this value, the High Limit Bit will turn ON.
High Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Greater Than or Equal To the High Limit parameter setting.
Low Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Less Than or Equal To this value, the Low Limit Bit will turn ON.
Low Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Less Than orEqual To the Low Limit parameter setting.
Low Low Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Less Than or Equal To this value, the Low Low Limit Bit will turn ON.
Low Low Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Less Than or Equal To the Low Low Limit parameter setting.
Deviation Limit Yellow	Numerical Tag/ Constant	Optional	One of two user definable Alarms that show when the Error is out of a specified range. The value specified is reflected as the range above AND below the Set Point. If used, when the Error reaches this value, the Deviation Limit Yellow Bit will turn ON.
Deviation Limit Yellow Bit	Boolean Tag	Optional	Turns ON if the Deviation Limit Yellow is reached.
Deviation Limit Orange	Numerical Tag/ Constant	Optional	One of two user definable Alarms that show when the Error is out of a specified range. The value specified is reflected as the range above AND below the Set Point. If used, when the Error reaches this value, the Deviation Limit Orange Bit will turn ON.
Deviation Limit Orange Bit	Boolean Tag	Optional	Turns ON if the Deviation Limit Orange is reached.
Rate of Change	Numerical Tag/ Constant	Optional	When used, if the Process Variable Changes at a Rate greater than this value (in Input Units per Second), the Rate of Change Bit will turn ON.
Rate of Change Bit	Boolean Tag	Optional	Turns ON if the Rate of Change Setting is reached.
Alarm Hysteresis	Numerical Tag/ Constant	Optional	Allows the user to specify a Numeric value that will offset the OFF transition of your process Alarms. The Alarm Bits will transition ON at the user defined value, but will add the Hysteresis value before it transitions OFF. This helps prevent cycling of the Alarm Bit as a noisy PV bounces in and out of the Alarm range. As the Process Variable increases above the setpoint, the high side Alarms (Alarms above the setpoint) will transition from OFF to ON at the desired setpoint. As the Process Variable begins to correct itself and decrease, they will transition from ON to OFF at the setpoint – Hysteresis Value. As the Process Variable decreases below the setpoint, the low side Alarms (Alarms below the setpoint) will transition from OFF to ON at the desired setpoint. As the Process Variable begins to correct itself and increase, they will transition from ON to OFF at the setpoint + Hysteresis Value.

Major Alarms Tab Configuration

When PID Loop Instruction is selected the PID Loop Configuration window opens with the Major Setup Tab opened by default. Click on the Major Alarms Tab to see the Configuration options for Major Alarms shown below.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Major Alarms Tab

Notes

High High Limit Value

Enter a Value or Tag for High HighLimit Value.

High High Limit Bit

Enter a Tag for High High Limit Bit.

High Limit Value

Enter a Value or Tag for HighLimit Value.

High Limit Bit

Enter a Tag for High Limit Bit.

Low Limit Value

Enter a Value or Tag for Low Limit Value.

Low Limit Bit

Enter a Tag for Low Limit Bit.

Low Low Limit Value

Enter a Value or Tag for Low LowLimit Value.

Low Low Limit Bit

Enter a Tag for Low Low Limit Bit.

Deviation Limit Yellow

Enter a Value or Tag for Deviation Limit Yellow.

Deviation Limit Yellow Bit

Enter a Tag for Deviation Limit Yellow Bit.

Deviation Limit Orange

Enter a Value or Tag for Deviation Limit Orange Bit.

Deviation Limit Orange Bit

Enter a Tag for Deviation Limit Orange Bit.

Rate of Change

Enter a Value or Tag for Rate of Change.

Rate of Change Bit

Enter a Tag for Rate of Change Bit.

Alarm Hysteresis

Enter a Value or Tag for the Alarm Hysteresis.

Use Structure

Select to use a Predefined Structure for this instruction.

Cascade Mode: Minor Setup Tab

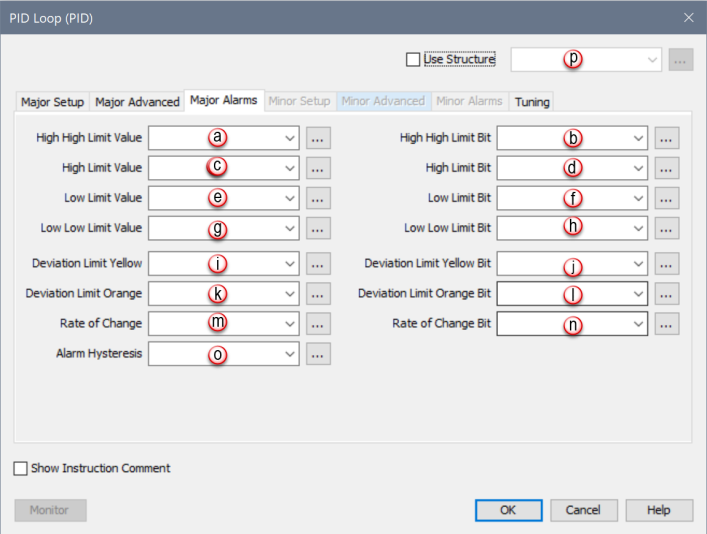
This Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. This Tab provides all the Main Configuration parameters for the Cascaded Loop.

Minor Setup Tab Parameters

Parameter	Parameter Type	Requirements	Description
Cascade Mode SP	Numerical Tag/	Must Have	The Set Point (SP) generated by the Major Loop Control Output when Cascade mode Control is Enabled.
Auto Mode SP	Numerical Tag/ Constant	Must Have	The Minor Loop Set Point when Cascade Mode Control is not Enabled.
Process Variable	Numerical Tag/ Constant	Must Have	A Feedback Signal that monitors the current state of the Process.
Input Range Max	Numerical Tag/ Constant	Must Have	The reference point that represents 100% in calculating the scaling factor to apply to the measured Error (SP-PV) before PID calculations. This value will not clamp the inputs. Typical value is the maximum possible input. See Note 1 below
Input Range Min	Numerical Tag/ Constant	Must Have	The reference point that represents 0% in calculating the scaling factor to apply to the measured Error (SP-PV) before PID calculations. This value will not clamp the inputs. Typical value is the minimum possible input. See Note 1 below
Process Output	Numerical Tag	Must Have	The result of the Loop Calculation, which drives the Process to the desired Set Point.
Output Range Max	Numerical Tag/ Constant	Must Have if Analog out selected.	The reference point that represents 100% in calculating the scaling factor to apply to the Process Output after PID calculations. This value will not clamp the Process Output. Typical value is the maximum possible Output. See Note 1 and Note 2 below
Output Range Min	Numerical Tag/ Constant	Must Have if Analog out selected.	The reference point that represents 0% in calculating the scaling factor to apply to the Process Output after PID calculations. This value will not clamp the Process Output. Typical value is the minimum possible Output. See Note 1 below
Output Upper Limit	Numerical Tag/ Constant	Must Have	Process Output will be clamped to no greater than this value. Typical value is the maximum possible Output.
Output Lower Limit	Constant	Must Have	Process Output will be clamped to no less than this value. Typical value is the minimum possible Output.
Proportional (Gain)	Numerical Tag	Must Have	This value is directly Proportional to the control effect, meaning an increase to the Proportional value (sometimes referred to as Gain) will increase the control output for forward acting Loops and decrease the control output for reverse acting Loops. In the PID Algorithm, the Proportional Gain is multiplied by the Error during each sample and added to the Bias Term. Formula: Pgain * Error (SP-PV) Where: Pgain = Proportional Gain Error = The value difference between Process Variable (PV) and Setpoint (SP). SP = Set Point is the desired Setting for the controlled Process. PV = Process Variable is the Feedback Signal that monitors the current state of the Process.
Integral (Reset) Time	Numerical Tag	Must Have	This value is a Time constant that is used to remove Error after the control output has reached a steady state. The Integral Time setting is inversely Proportional to the control effect, meaning as the value increases, the rate at which the Error is removed decreases. In the PID Algorithm, the Integral Term is multiplied by the accumulated Error and added to the control output. Formula: C _IT ∑e Where: C_IT = Coefficient of Integral Time ∑e = Summation of Error per sample
Derivative (Rate) Time	Numerical Tag	Optional	In many cases this parameter is not required to achieve stable Loop operation and is highly sensitive to noise in the Error Term. This value is directly Proportional to the control effect, meaning that the higher the Derivative Term setting, the quicker the Error will be removed. In the PID Algorithm, the Derivative Term formula is added to the control output. Formula: C_{DT *} e + Initial Output Where: C_DT = Coefficient of Derivative Time e = Current Error - Previous Error

Note 1: This value will be read by the instruction only during an OFF to ON transition of the Enable.

Note 2: To see a change in the Process Output, a value greater than zero must be entered into this parameter.

Minor Setup Tab Configuration

When PID Loop Instruction is selected, the PID Loop Configuration window opens with the Major Setup Tab opened by default. This Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. Therefore, select Cascade Mode first and then click on the Minor Setup Tab to see the Configuration options for Minor Setup shown below.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Minor Setup Tab

Notes

Cascade Mode SP

Displays the Cascade Mode Set Point Tag.

Auto Mode Set Point

Enter a Value or Tag for Auto Mode Set Point. (When Cascade Mode is Not Enabled).

Process Variable

Enter a Value or Tag for Process Variable.

Input Range Max

Enter a Value or Tag for Input Range Max.

Input Range Min

Enter a Value or Tag for Input Range Min.

Process Output

Enter a NumericTag for Process Output based on Output type.

Output Range Max

Enter a Value or Tag for Output Range Max.

Output Range Min

Enter a Value or Tag for Output Range Min.

Output Upper Limit

Enter a Value or Tag for Output Upper Limit.

Output Lower Limit

Enter a Value or Tag for Output Lower Limit.

Gain (Proportional)

Enter a Value or Tag for Proportional Gain.

Reset (Integral) Time

Enter a Value or Tag for Reset Time.

Rate (Derivative) Time

Enter a Value or Tag for Rate Time.

Use Structure

Select to use a Predefined Structure for this instruction.

Cascade Mode: Minor Advanced Tab

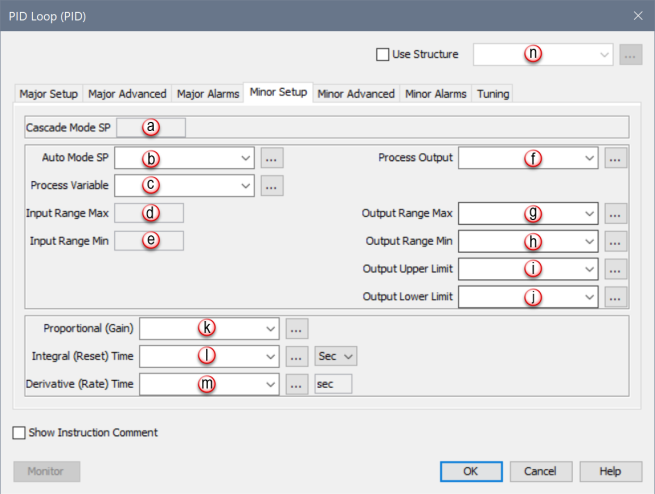
This Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. The Minor Advanced Tab provides all the Advanced Configuration parameters for the Cascaded Loop.

Minor Advanced Tab Parameters

Parameter	Parameter Type	Requirements	Description
Sample Rate (ms)	Numerical Tag/ Constant	Must Have	Identifies how often the instruction will calculate a new output value. Setting the Sample Rate shorter than the scan time will cause the loop to calculate on every scan. The sample rate must be longer than the rate at which new PV data is available. If it is not, the Integral and Derivative affects could be erratic.
Error Squared	Boolean Tag/ Constant	Optional	Setting this bit will Square the Error. This can be useful for many processes by effectively diminishing the control effect on smaller Errors while maintaining the control effect on larger Errors. This can also be useful for reducing the effect of low frequency electrical noise in your process.
Loop Offset (ms)	Numerical Tag/ Constant	Must Have if Auto Mode is not selected	When set to Auto Mode, the CPU attempts to stagger the execution of PID Loops so they will occur on different scans. Loop Offset can be handled manually by assigning different Offset values to multiple PID Loops.
Process Output Percentage	Numerical Tag	Optional	The current Output Percentage on a scale of 0-100%.
Derivative Limit	Numerical Tag/ Constant	Optional	Multiplier that limits the Output adjustment applied by the Derivative term. 1 = 100% of Output scale, or No Limit (default). 0.5 = 50% of Output scale.
Bias Term	Numerical Tag	Optional	The Bias Term is the Current Integral Term + Initial Output. The Bias Term is a percentage value calculated by the instruction, which effectively creates a working region for the Control Output.
Freeze Bias	Radio Button	Optional	Default Setting is ON. Stops the Bias Term calculation when the Output value reaches the upper or lower limit (usually due to a disturbance). This setting prevents reset wind-up which can lead to overshooting the Set Point when a disturbance is removed.
Back Calculation	Radio Button	Optional	If the Output is calculated to be above or below the upper or lower limit, this option will adjust the Bias Term accordingly to make the Output equal to the limit. As soon as the process begins to recover, the loop will go directly into regulation. This anti-windup option is more conservative than Freeze Bias, typically less likely to overshoot but slower to recover from the disturbance.
Base the Derivative on Process Variable	Selectable Checkbox	Optional	When selected, uses the Derivative is based on changes in the Process Variable. When deselected the Derivative is based on changes in the Error term (SP – PV).
SP Accel Gain	Numerical Tag/ Constant	Optional	A value of 0 disables this function. The process monitors for a change in the set point value. If a set point change is detected, the difference from the new and old set points are multiplied by the SP Accel Gain value and then added to the Bias Term. This action is Edge triggered so it processes only once per change in the set point value.
Error Deadband	Numerical Tag	Optional	When used, the Error Deadband takes a range of Error near Zero and substitutes Zero as the value of the Error. Enter the value in Input Units.
Initialization Mode	Selectable Drop-down List	Check the PV Tracking checkbox or Select one from the list	Determine the state of the Process Variable and Bias Term at startup. SP = PV and Bias = Output. PV tracking check box selected. SP unchanged and Bias = Output SP unchanged and *Bias = (Output – KE) [Default] (where K = The Proportional Term and E = The Error Term) SP unchanged and Bias = Current (initialize with a Bump**)
Process Action	Selectable Drop-down List	Select one from the list	Determines how the Process reacts to the Output. The two choices are: Forward: As the Output increases so will the Process Variable. (i.e., heating loop) Reverse: As the Output increases the Process Variable will decrease. (i.e., cooling loop)

Minor Advanced Tab Configuration

When PID Loop Instruction is selected the PID Loop Configuration window opens with the Major Setup Tab opened by default. This Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. Therefore, select Cascade Mode first and then click on the Minor Advanced Tab to see the Configuration options for Minor Advanced shown below.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Minor Advanced Tab

Notes

Sample Rate (ms)

Enter a Value or Tag for Sample Rate.

Loop Offset (ms)

Only active if the Auto checkbox is not checked. Enter a Value or Tag for Loop Offset.

Auto

Click checkbox to let the program provide this value Automatically.

Derivative Limit

Enter a Value orTag for the Derivative Limit.

Bias Term

Enter a Tag for Bias Term.

SP Acceleration Gain

Enter a Boolean Tag for Feed Forward.

Error Deadband

Enter a Value or Tag for Error Deadband.

Process Action

Select a Process Action from the drop-down list. The choices are Forward or Reverse.

Error Squared

Enter a Value (0 or 1) or Tag for Error Squared.

Process Output Percentage

Enter a Tag for Process Output Percentage.

Freeze Bias

Click ON or OFF button to enable or disable this feature.

Back Calculation

Click button to enable this feature..

Base the Derivative on Process Variable

Click checkbox to enable this feature.

Initialization Mode: PV Tracking

Click checkbox to select PV tracking method.

Initialization Mode: Unchecked

Select a PV Tracking Mode from the drop-down list.

Use Structure

Select to use a Predefined Structure for this instruction.

Cascade Mode: Minor Alarms Tab

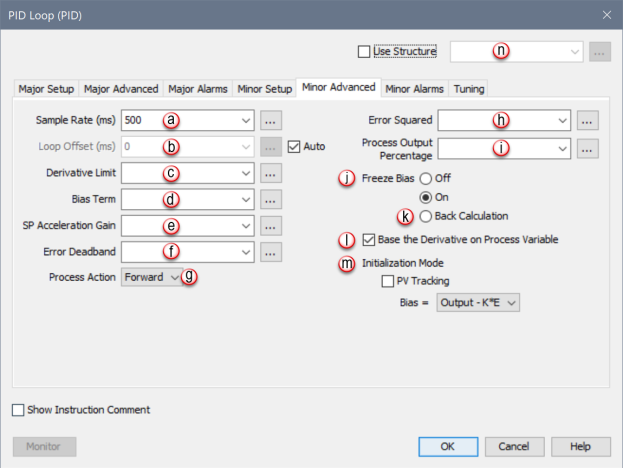
This Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. This Tab provides all the Minor Alarms Configuration parameters for the Cascaded Loop.

Minor Alarms Tab Parameters

Parameter	Parameter Type	Requirements	Description
High High Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Equal To or Greater Than this value, the High High Limit Bit will turn ON.
High High Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Equal To or Greater Than the High High Limit parameter setting.
High Limit Value	Constant	Optional	If used, when the Process Variable is Equal To or Greater Than this value, the High Limit Bit will turn ON.
High Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Equal To or Greater Than the High Limit parameter setting.
Low Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variable is Less Than or Equal To this value, the Low Limit Bit will turn ON.
Low Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Less Than or Equal To the Low Limit parameter setting.
Low Low Limit Value	Numerical Tag/ Constant	Optional	If used, when the Process Variableis Less Than or Equal To this value, the Low Low Limit Bit will turn ON.
Low Low Limit Bit	Boolean Tag	Optional	Turns ON if the Process Variable signal is Less Than or Equal To the Low Low Limit parameter setting.
Deviation Limit Yellow	Numerical Tag/ Constant	Optional	One of two user definable Alarms that show when the Error is out of a specified range. The value specified is reflected as the range above AND below the Set Point. If used, when the Error reaches this value, the Deviation Limit Yellow Bit will turn ON.
Deviation Limit Yellow Bit	Boolean Tag	Optional	Turns ON if the Deviation Limit Yellow is reached.
Deviation Limit Orange	Numerical Tag/ Constant	Optional	One of two user definable Alarms that show when the Error is out of a specified range. The value specified is reflected as the range above AND below the Set Point. If used, when the Error reaches this value, the Deviation Limit Orange Bit will turn ON.
Deviation Limit Orange Bit	Boolean Tag	Optional	Turns ON if the Deviation Limit Orange is reached.
Rate of Change	Numerical Tag/ Constant	Optional	When used, if the Process Variable Changes at a Rate greater than this value (in Input Units per Second), the Rate of Change Bit will turn ON.
Rate of Change Bit	Boolean Tag	Optional	Turns ON if the Rate of Change Setting is reached.
Alarm Hysteresis	Numerical Tag/ Constant	Optional	Allows the user to specify a Numeric value that will offset the OFF transition of your process Alarms. The Alarm Bits will transition ON at the user defined value, but will add the Hysteresis value before it transitions OFF. This helps prevent cycling of the Alarm Bit as a noisy PV bounces in and out of the Alarm range. As the Process Variable increases above the setpoint, the high side Alarms (Alarms above the setpoint) will transition from OFF to ON at the desired setpoint. As the Process Variable begins to correct itself and decrease, they will transition from ON to OFF at the setpoint – Hysteresis Value. As the Process Variable decreases below the setpoint, the low side Alarms (Alarms below the setpoint) will transition from OFF to ON at the desired setpoint. As the Process Variable begins to correct itself and increase, they will transition from ON to OFF at the setpoint + Hysteresis Value.

Minor Alarms Tab Configuration

When PID Loop Instruction is selected the PID Loop Configuration window opens with the Major Setup Tab opened by default. The Minor Alarms Tab is only active when the Cascade Mode selection found in the Major Advanced Tab is selected. Therefore, select Cascade Mode first and then click on the Minor Alarms Tab to see the Configuration options for Minor Alarms shown below.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Minor Alarms Tab

Notes

High High Limit Value

Enter a Value or Tag for High High Limit Value.

High High Limit Bit

Enter a Tag for High High Limit Bit.

High Limit Value

Enter a Value or Tag for High Limit Value.

High Limit Bit

Enter a Tag for High Limit Bit.

Low Limit Value

Enter a Value or Tag for Low Limit Value.

Low Limit Bit

Enter a Tag for Low Limit Bit.

Low Low Limit Value

Enter a Value or Tag for Low Low Limit Value.

Low Low Limit Bit

Enter a Tag for Low Low Limit Bit.

Deviation Limit Yellow

Enter a Value or Tag for Deviation Limit Yellow.

Deviation Limit Yellow Bit

Enter a Tag for Deviation Limit Yellow Bit.

Deviation Limit Orange

Enter a Value or Tag for Deviation Limit Orange Bit.

Deviation Limit Orange Bit

Enter a Tag for Deviation Limit Orange Bit.

Rate of Change

Enter a Value or Tag for Rate of Change.

Rate of Change Bit

Enter a Tag for Rate of Change Bit.

Alarm Hysteresis

Enter a Value or Tag for the Alarm Hysteresis.

Use Structure

Select to use a Predefined Structure for this instruction.

PID External Auto Tune

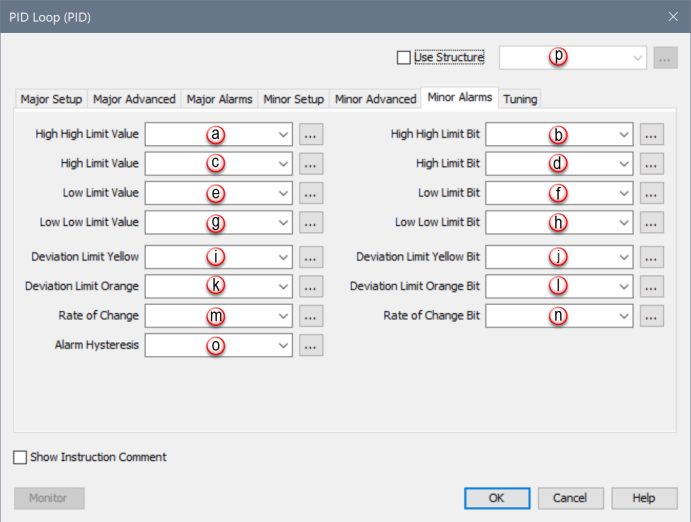
You can use External Auto Tune to start and stop an auto-tuning session through an external HMI/SCADA. For a description of the Auto Tune process, please refer to Auto Tune Settings under PID Tuning.

Configuration:

Configure the External Auto Tune control/status parameters using the Tuning Tab located on the PID Loop (PID) screen.

Parameter Configuration Table

PID Loop

Instruction

(PID)

Tuning Tab

Notes

Loop Type

Enter a Value or Tag for Loop Type.

Tuning Type

Enter a Value or Tag for Tuning Type

PV Deadband

Enter a Value or Tag for PV Deadband.

Initial PV Bump

Enter a Value or Tag for Initial PV Bump..

Control

Enter a Tag for Tuning Control

Status

Enter a Value or Tag for Tuning Status.

Use Structure

Enter a Value or Tag for Low Low Limit Value.

Auto-tune Parameters:

Loop Type (Integer): Integer tag or constant to select Major or Minor loop to tune. 0: Major, 1: Minor. Minor loop is a valid option only when PID loop is configured for Cascade Mode.
Tuning Type (Integer): Select the Tuning Method.
3: PI (returns Proportional and Integral terms only) or
7: PID (returns Proportional, Integral, and Derivative terms)
PV Deadband (Integer): This applies a Deadband (buffer zone) around the value of the Process Variable at the time you initiate the Auto Tune cycle. This value should be larger than the typical noise on the PV input. This is used to help the Auto Tune avoid reacting to the PV noise and miscalculating or moving into the next cycle prematurely.
Initial PV Bump (Integer): When you begin the Auto Tune procedure the Output will turn ON and remain ON until the Initial PV Bump value is met. At that time it will change direction and begin the three cycle Auto Tune profile.
Control (Boolean): Start/Stop External Auto Tune.
Status (Integer): Returns current Auto Tune status:

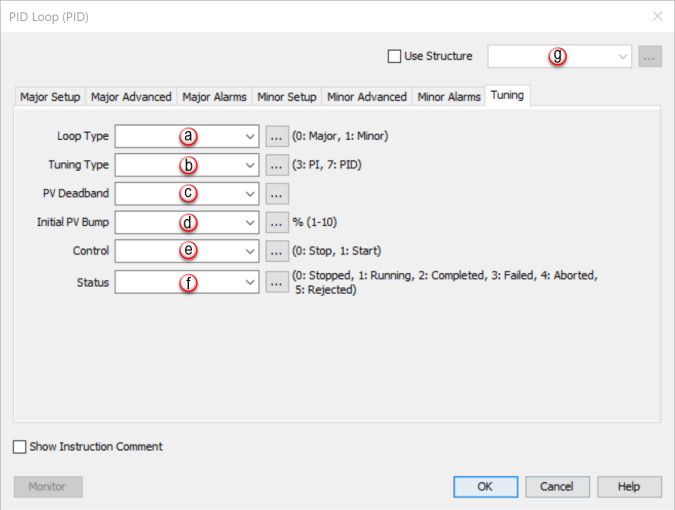
0: Stopped External Auto Tune is stopped/disabled

1: Running External Auto Tune is currently running

2: Completed External Auto Tune has completed successfully

3: Failed External Auto Tune has failed

4: Aborted External Auto Tune was aborted by user

5: Rejected External Auto Tune was rejected

What is PID?

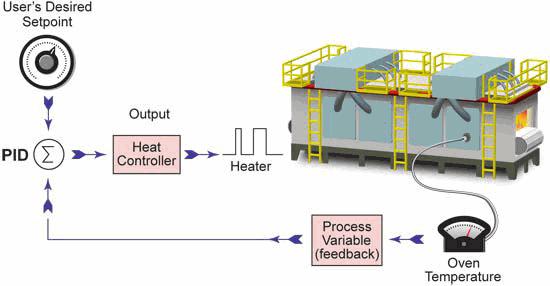
The letters PID refer to Proportional, Integral, Derivative control. PID is a Control Algorithm used to closely control processes such as temperature, mixture, position, and velocity. The Proportional Gain portion takes care of the magnitude of the Error and is calculated using terms of percent of full scale, not counts or engineering units. The Integral takes care of small Errors over time. The Derivative compensates for the Rate of Error change.

Consider this example application. For simplification, only Proportional Gain is used. An oven is being controlled by an SCR-driven electric heater using a 4-20mA Output channel. This Analog Output is the Process Output. The temperature of the oven is measured using an RTD via a P3-08RTD module. This Input is the Process Variable (PV). The desired temperature of the oven is the Set Point (SP).

For Input values such as Set Point (SP) and Process Variable (PV), full scale is the span between Input Range Min and Input Range Max of the PID instruction. In this example, the P3-08RTD provides temperature in degrees directly, not counts, where every four degrees is 1% of full scale.

If the Set Point is 300 and the Process Value (RTD) is 292, the Error would be 8 degrees. With the scaling set by Input Range Min and Input Range Max, 8 degrees Error represents 2% of the Input range. The2% is multiplied by Proportional Gain. If the Proportional Gain is 10, the result would be 2%*10=20%. So with these variables applied, Proportional Gain alone would drive the Process Output to 20% of full scale, with full scale being defined by the Output Range Max and Output Range Min tags.

The SCR controlling the heater is driven by a 4-20mA Analog Output point accepting values of 0-65535. Output Range Min and Output Range Max might be set to 0 and 65535 respectively. In the above example, with the Error being 8 degrees, the Output would be driven to 20% of full scale or 13107 counts, sending 7.2mA to the SCR.

Note: If the Proportional Gain is set too Low, the PID Control will be slow and ineffective in driving the Output to correct for Errors between the Process and Set Point. If set too High, the PID will produce oscillations as the Process Variable approaches the Set Point.

Integral Time: Unless the process naturally has the correct Integrating Properties, some Offset will result between the Process Variable and SetPoint. The Integral Gain will correct or reset this Error or Offset.

The CPU uses 1/Ts (the sample rate), which produces a reciprocal effect, meaning the larger the number the less effect the Integral Gain will have.

Note: After the Proportional Gain is set, if the Integral Gain is set too Low (too large of a value), then the PID control will be ineffective correcting Process Variable and Set PointOffsets. If set too High (too small a value), then the Process Variable will overshoot the Set Point and oscillations will occur.

Derivative (Rate):Proportional Gain and Integral Gain can handle many processes. However, when large disturbances are introduced into the process, this creates sudden and large errors between the Process Variable and Set Point. The Derivative value will react to these sudden disturbances and attempt to correct the error while maintaining the stability of the loop.

Note: The larger the number, the more effective the Rate will respond to Process Upsets. However, the Rate should be set just high enough to help the effects of Process Upsets. If the Rate is set too High, the Proportional and Integral Gain normal action will be adversely effected and the Proportional and Integral Gain control will become sluggish and ineffective.

PID Algorithm

The Proportional Integral Derivative (PID)Algorithm is widely used in process control. The PID method of control adapts well to electronic solutions, whether implemented in analog or digital (CPU) components. The CPU implements the PID equations digitally by solving the basic equations in software. I/O modules serve only to convert electronic signals into digital form (or vice versa).

The PID Algorithm causes the PID equation to calculate the Control OutputMn:

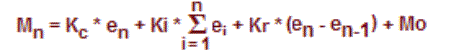
In the formula below, the sum of the Integral Terms and the Initial Output are combined into the Bias Term (Mx). Using the Bias Term, we define formulas for the Bias and Control Output as a function of sampling time:

The PID Algorithm variables and related variables are:

Ts = Sample Rate
Kc = Proportional Gain
Ki = Kc * (Ts/Ti) Coefficient of Integral Term
Kr = Kc * (Td/Ts) Coefficient of Derivative Term
Ti = Reset Time (Integral Time)
Td = Rate Time (Derivative Time)
SPn = Set Point for Sampling Time “n” (SP value)
PVn = Process Variable for Sampling Time “n” (PV)
en = SPn – PVn = Error Term for Sampling Time “n”
M0 = Control Output for Sampling Time “0”
Mn = Control Output for Sampling Time “n”

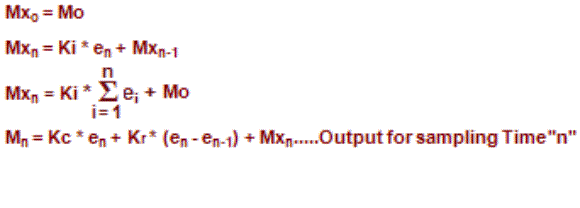
Detailed analysis of these equations will be found in most good textbooks on Process Control. At a glance, we can isolate the parts of the PID Algorithm that correspond to the P, I, and D terms, and the Bias as shown below.

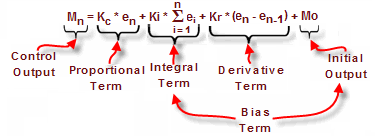
The Initial Output is the Output value assumed from Manual Mode control when the Loop transitions to Auto Mode. The sum of the Initial Output and the Integral Term is the Bias Term, which holds the Position of the Output.

PID Algorithm Example

In this example, we will apply the PID algorithm to a temperature control loop. The loop is maintaining the temperature of an oven. The desired temperature of the oven is 350˚F. For this loop, we will set the algorithm’s parameters as follows:

Kr = 0 (To achieve this, set the Derivative Time (Td) to zero. This will make the loop a PI controller, we will look at the derivative affect later.)
Kc = 3 (Proportional Gain)
Ts = 1 second (Sample Rate)
Ki = 0.1 (To achieve this, set Ti or Integral Time to 30 seconds, Ki = 3*1/30 = 0.1)
M(0) = 30 (Initial Control Output) At sample zero, the loop has an initial control output (M(0)) of 30.

Looking at the graph below, we can see that with this control output the loop has been stable at 350˚F for the first five samples.

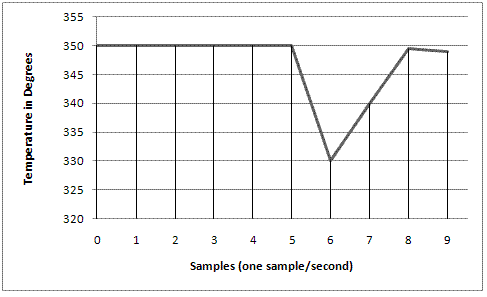
After the fifth sample, the oven door is opened and an item is placed inside. This causes a drop of 20˚F in our actual temperature which is seen at sample six. Therefore, the error in the system at sample six is calculated to be: e(6) = SP-PV = 350 - 330 = 20. Also, at this point the sum of all the sample errors for the system will equal:

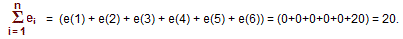
Using the parameters and calculated values above, the algorithm for the loop at sample six would become:

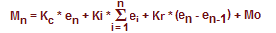
M(6) = (3*20)+(0.1*20)+(0*(20-0))+30

M(6) = 60 + 2 + 30

M(6) = 92 - At this point, there is an increase in the control output of 62 from the initial control output and the proportional term is the main force driving this increase with a value of 60.

As discussed in the What is PID? section of this chapter, the control output will be converted to an analog value (0-10V, 4-20mA) that is fed to an end device. In our example, that device is an SCR-driven electric heater. As the control output drives the temperature toward the setpoint, we see at sample seven that the error has decreased to: e(7) = SP-PV = 350 - 340 = 10. Also at this point, the sum of all the sample errors will equal 30 and the algorithm will become:

M(7) = (3*10)+(0.1*30)+(0*(10-20))+30

M(7) = 30 + 3 + 30

M(7) = 63 - Here we see that as the error is corrected, the control output will decrease due to the drop in the proportional term. However, the integral term has risen slightly.

At sample eight, the oven temperature has recovered to 349.5˚F leaving a minimal error of: e(8) = SP-PV = 350 - 349.5 = 0.5. The sum of all sample errors is now 30.5 and the control output equals:

M(8) = (3*0.5)+(0.1*30.5)+(0*(0.5-10))+30

M(8) = 1.5 + 3.05 + 30

M(8) = 34.55 - At this point, the proportional term has dropped off considerably and the integral bias has exceeded the proportional gain in controlling the output.

When tuning a loop, it is important to remember that with large errors the proportional term will drive the output and with small errors the integral term will take control.

The last item to consider when dealing with a PID controlled system is the rate of change in the process variable. With our example, the rate of change is very rapid when the door is opened. A 20˚F drop within one second. With very rapid changes, there is a risk of instability in the loop and the derivative term attempts to alleviate this while aiding in the correction. The derivative term will look at the difference between the error now and the error before, determine how rapidly the process variable is deviating from or correcting to the setpoint and adjust the output accordingly. If we add a derivative coefficient of Kr = 0.5 (set the Derivative Time (Td) to 0.167 seconds, Kr = 3*0.167/1 = 0.5) to the samples in our discussion they become:

M(6) = (3*20)+(0.1*20)+(0.5*(20-0))+30

M(6) = 60 + 2 + 10 + 30

M(6) = 102

M(7) = (3*10)+(0.1*30)+(0.5*(10-20))+30

M(7) = 30 + 3 - 5 + 30

M(7) = 58

M(8) = (3*0.5)+(0.1*30.5)+(0.5*(0.5-10))+30

M(8) = 1.5 + 3.05 - 4.75 + 30

M(8) = 29.8

Looking at sample eight (M(8)) and disregarding the initial output (M(0)), we can see that with the derivative influence the bias applied to the control output dropped from 4.55 to -0.2. The derivative term determined that the process variable was approaching the setpoint at a very rapid rate and dampened the control output to avoid an overshoot of the setpoint.

Cascade PID Operation

Cascade PID Loop Control can improve your system performance when compared to a Single Loop Control if your process demonstrates one of the following characteristics:

When disturbances in a secondary process directly affects your primary process.

In this case a Cascade Controlled System can limit the effects of disturbances on the second process variable on the primary output.

When the Process Gain or the actuator of your secondary process is Non-linear.

In this case a Cascade Controlled System can limit the effect of variations in the secondary system on the main control system's performance.

There are three modes of operation to consider when operating a Cascade Loop process:

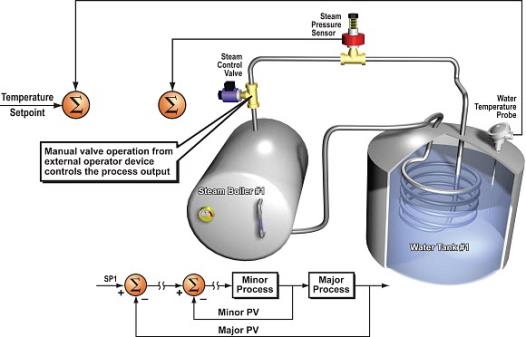
Manual Mode Operation is when the PID Loop instruction is enabled (ladder input), but it is not in Auto Mode(ladder input) or Cascade Mode(Cascade Mode Enable control tag).

In Manual Mode the algorithm is not calculated and the user can write values to the Process Output variable (Steam Control Valve) as shown in the diagram below.

Set Point and Process Variables are updated but not acted upon.

Alarms are active in Manual Mode.

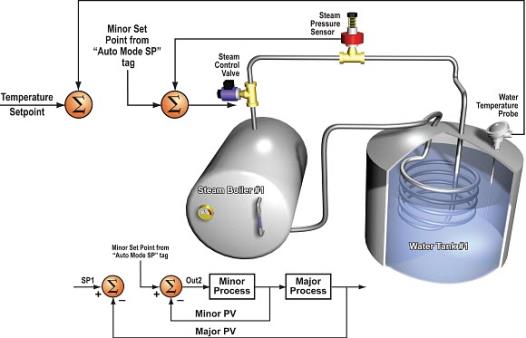
Auto Mode Operation is when the PID Loop instruction is enabled (ladder input), set to Auto Mode (ladder input) but not set to Cascade Mode (Cascade Mode Enable control tag).

In Auto Mode both the Major andMinor Loopsare calculated as individual Loops. The Minor Loop set point is pulled from theAuto Mode SP Tag defined in theMinor Setup Tabof the instruction and not from theMajor Loops Output, as shown in the diagram below.

Set Point and Process Variables are updated but not acted upon.

Alarms are active in Auto Mode.

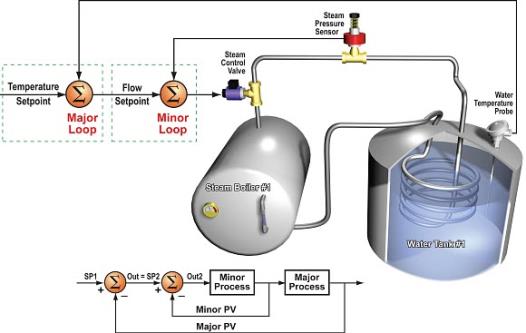
Cascade Mode Operation is when the PID Loop instruction is enabled (ladder input), set to Auto Mode (ladder input), and set to Cascade Mode (Cascade Mode Enable control tag).

In Cascade Mode both the Major and Minor Loops are calculated as a CombinedLoop. The Minor Loop set point is pulled from the Major Loop's Output as shown in the diagram below.

Time-Proportioning Control

The PID Loop Control Output signal generates a smooth signal across a numerical range. The Control Output value is suitable to drive an Analog Output Module, which connects to the process. In the process control field, this is called continuous Control, because the output is on (at some level) continuously.

While continuous Control can be smooth and robust, the cost of the Loop components (such as actuators, heater amplifiers) can be expensive. A simpler form of Control is called time-proportioning Control or ON/OFF Control. This method uses actuators that are either ON or OFF (no in-between). Loop components for ON/OFF-Based Control systems are lower cost than their continuous Control counterparts.

The diagram below shows a hot-air balloon following a path across some mountains. The desired path is the Setpoint. The balloon pilot turns the burner ON and OFF alternately, which is his Control Output. The large mass of air in the balloon effectively averages the effect of the burner, converting the bursts of heat into a continuous effect: slowly hanging balloon temperature and ultimately the altitude, which is the Process Variable.

Time-Proportioning Control approximates continuous Control by virtue of its duty-cycle – the ratio of ON time to OFF time. The following figure shows an example of how duty cycle approximates a continuous level when it is averaged by a large process mass.

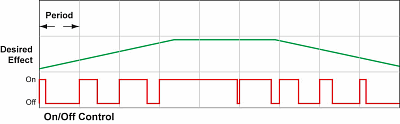
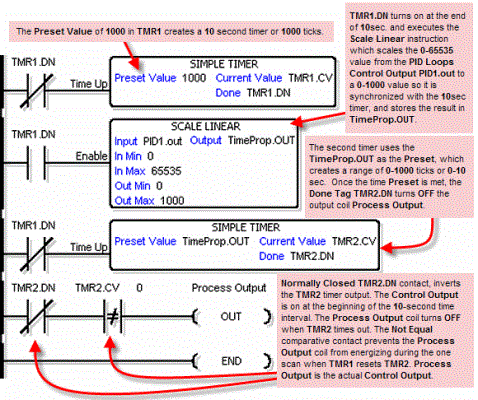
The example logic below shows how you would convert the smooth continuous Control signal from the PID Control Output to a pulsing Time-Proportioning Control for applications that require it.

The example logic below shows how you would convert the smooth continuous Control signal from the PID Control Output to a Pulsing Time-Proportioning Control for applications that require it.

The example program uses two timers to generate ON/OFF Control. It makes the following Assumptions, which you can alter to fit your application:

The data format of the Control Output is Signed 32 Bit Integer
The range of the Control Output is 0 - 65535
The ON/OFF Control Output is Tag ‘TimeProp.OUT’.

The Control program must Match the resolution of the Output to the resolution of the Time Interval. The Time Interval for one full cycle of the ON/OFF waveform is 10 seconds.

Note: Some processes change too fast for Time Proportioning Control. Consider the speed of your process when you choose this Control method. Use continuous Control for processes that change too fast for Time Proportioning Control.

0: Stopped	External Auto Tune is stopped/disabled
1: Running	External Auto Tune is currently running
2: Completed	External Auto Tune has completed successfully
3: Failed	External Auto Tune has failed
4: Aborted	External Auto Tune was aborted by user
5: Rejected	External Auto Tune was rejected

PID Loop (PID) Instruction

Purpose

Instruction Parameters

Major Setup Tab Parameters

Major Setup Tab Configuration

Instruction

(PID)

Major Setup Tab

Notes

Major Advanced Tab Parameters (Common configuration parameters for more Advanced applications)

Major Advanced Tab Configuration

PID Loop

Instruction

(PID)

Major Advanced Tab

Notes

Major Alarms Tab

Major Alarms Tab Parameters

Major Alarms Tab Configuration

PID Loop

Instruction

(PID)

Major Alarms Tab

Notes

Cascade Mode: Minor Setup Tab

Minor Setup Tab Parameters

Minor Setup Tab Configuration

PID Loop

Instruction

(PID)

Minor Setup Tab

Notes

Cascade Mode: Minor Advanced Tab

Minor Advanced Tab Parameters

Minor Advanced Tab Configuration

PID Loop

Instruction

(PID)

Minor Advanced Tab

Notes

Cascade Mode: Minor Alarms Tab

Minor Alarms Tab Parameters

Minor Alarms Tab Configuration

PID Loop

Instruction

(PID)

Minor Alarms Tab

Notes

PID External Auto Tune

Configuration:

PID Loop

Instruction

(PID)

Tuning Tab

Notes

Auto-tune Parameters:

What is PID?

PID Algorithm

The PID Algorithm variables and related variables are:

PID Algorithm Example

Cascade PID Operation

Time-Proportioning Control

Application Example

Example of a Process Using PID to Control the Oven Temperature

Rung Example